串、数组、广义表
串
与栈和队列相似,串是内容受限的线性表,串的元素只能是字符
- 串中任意个连续字符组成的子序列称为该串的子串,真子串指不包含自身的所有子串
串的存储结构
顺序存储
1 |
|
- 加一使位序与下标相等,
data中第一个元素闲置不用,便于后续的计算
链式存储
1 |
|
- 使用块链结构,一块的大小为
CHUNKSIZE,以此来提高存储密度
串的模式匹配——KMP算法
确定主串中所含子串第一次出现的位置
详见【最浅显易懂的 KMP 算法讲解】 https://www.bilibili.com/video/BV1AY4y157yL/?share_source=copy_web&vd_source=fbe4b0e6c9f599f2e20ea27ac67af734
首先根据子串得出一个next数组,用来表示当匹配进行到该处时应该跳过子串前面的多少个字符,主串的i永远不递减
KMP算法思路是,当发现某个字符不匹配时,根据已经知道之前遍历过的字符来避免暴力算法中的回退步骤
已知next
1 | int KmpSearch(char main[], char child[],int next[], int slen, int clen) { |
当匹配时,i和j都加一
当匹配失败时,若j为零则
i++;若j不为零,会根据最后一个匹配的字符的next值即next[j - 1]来作为j的值,此时i不加一判断是否子串完全匹配成功,因为如果成功一定会执行子串最后一个字符匹配成功的结果,导致
j++,此时j == clen最后
return的值是子串的第一位在主串中的位置
getNext
1 | void getNext(char ch[], int len, int next[]) { |
- 从
i = 1开始,与第prefix_len位比对,初始为第0位 - 若相同则
i与prefix_len均加一,并将prefix_len的值赋给next[i] - 不相同则判断next数组上一个元素的值即
prefix_len,为零则给next[i]赋值为零 - 若
prefix_len不为零,以ABACABAB为例,进行至最后的B时,此时prefix_len = 3,最后的ABA与子串开头是相同的,因此前缀也相同,将prefix_len回溯为next[prefix_len - 1],此时i不变,继续进行循环
test
1 | int main() { |
- 结果为
0 0 1 0 1 2 3 2 && 4
数组
按照一定格式排列起来的,具有相同类型的数据元素的集合
由于数组长度固定且一般不做插入和删除操作,因此一般都用顺序存储来表示
顺序存储
数组可以是多维的,但存储数组的内存单元是一维的,因此在存储之前需要将多维关系映射到一维关系,这样就产生了两种存储二维数组的方法,分别为以行序为主序和以列序为主序
特殊矩阵的压缩存储
值相同的元素很多且呈某种规律分布或零元素多的矩阵不适宜常规存储,要进行压缩存储
压缩存储即为多个相同的非零元素只分配一个存储空间,对零元素不分配空间
对存在大量元素为零的矩阵(稀疏矩阵)的存储可以用三元组存储,格式为(i, j, aij),得出来的三元组顺序表中第零位用来存储总行数,总列数与元素个数
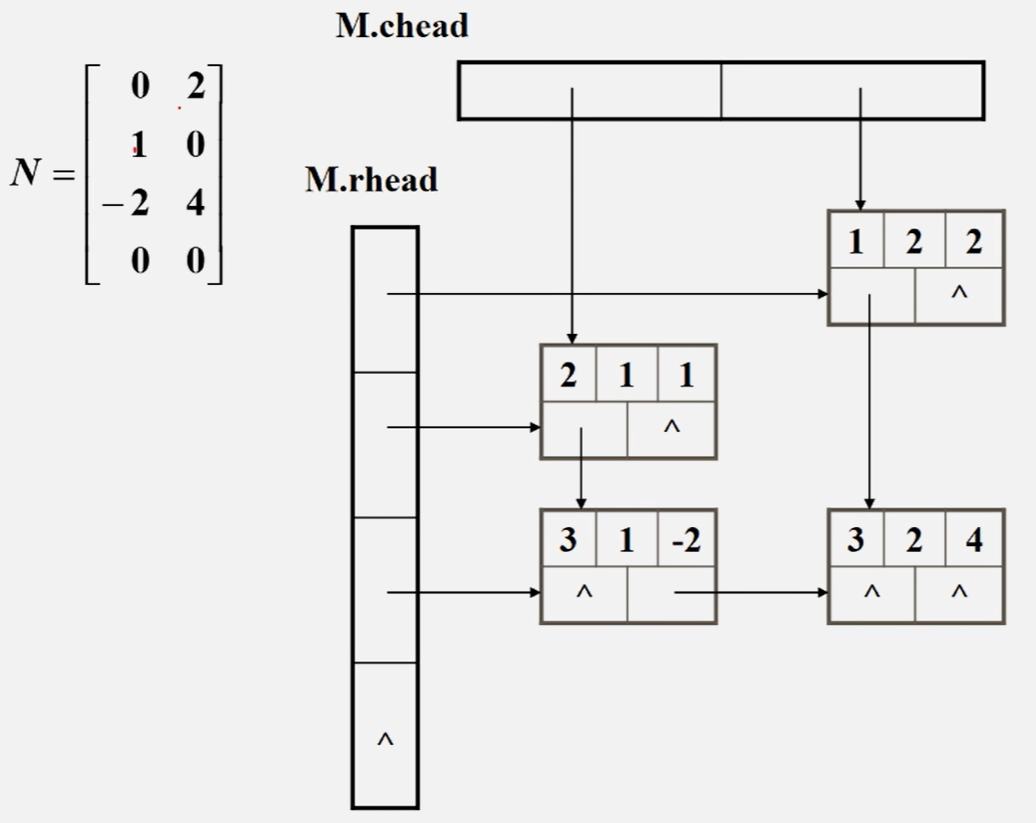
对于稀疏矩阵也有相关的链式存储结构——十字链表
在十字链表中,每一个非零元素用节点表示,结点除了row,col,value外还有两个域right,down,分别用来链接该元素同一行中下一个非零元素与同列中下一个非零元素
矩阵的行数与列数分别就是需要的行头指针与列头指针的数量,通过各个行头指针与列头指针将元素链接起来便于查找(真麻烦啊)
广义表
广义表的每个元素是一个原子,或是一个广义表。广义表一般记为LS = (a1, ..., an)
- 表头:若LS非空,则第一个元素
a1就是表头 - 表尾:除表头之外的其他元素组成的表,
(a2, ..., an)是表尾,表尾不是最后一个元素,而是一个子表
广义表是线性表的推广,线性表是广义表的特例








